本文共 4532 字,大约阅读时间需要 15 分钟。
前言
2020年,互联网裁员潮下,我度过了人生中最清晰的半年。
今年我本命年,熬过了程序员35的坎,却在36岁被公司破产来了当头一棒,领完了当月份的工资,老板,也是我哥们的老李走进我的办公室,没有迂回地通知我,公司倒了。
老李陷进沙发里,用手抹了把脸,看上去很疲惫。
三年前公司还在装修的时候,我过来搭把手看一看,老李叉着腰指着同一套沙发,意气风发的说:“哥们专门给你配的,这小沙发花了我两万,咱们以后光明未来的起点就在这儿了!”
不过三年,创业失败,我们又要找新的起点。
面试官:说说view中的事件分发?
android中事件分发机制是android中常见的问题,一般大家都知道view的分发事件是从view的Viewgroup(Parent)#dispatchTouchEvent到Viewgroup(Parent)#onInterceptTouchEvent再到View#dispatchTouchEvent,然后到view的onTouchEvent,最后又回到了Viewgroup(Parent)#onTouchEvent。如果大家记不住方法名,可以直接说先是parent的分发到拦截再到view的分发,再到view的消费,最后到parent的消费
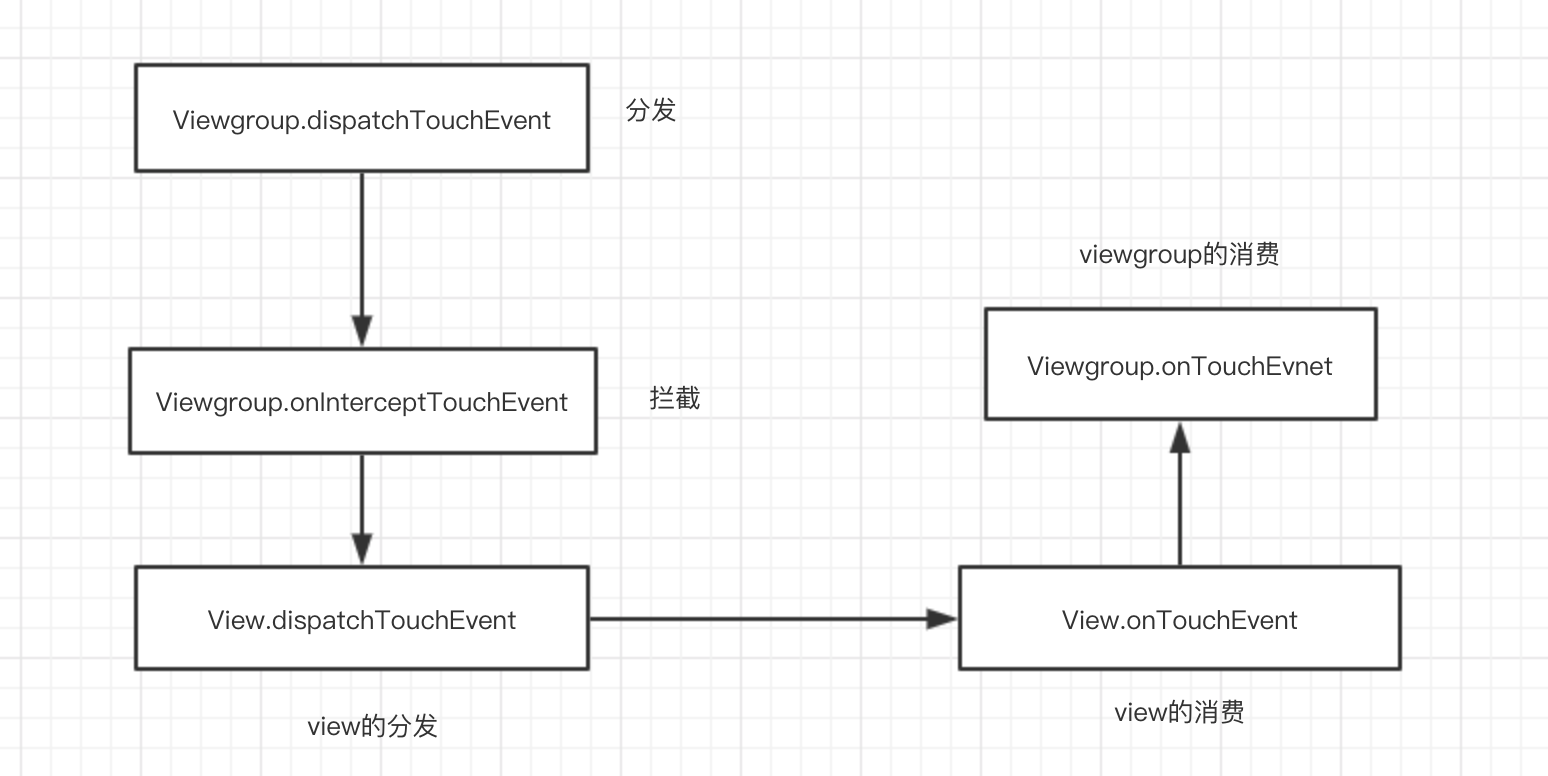
viewgroup分发
这样回答肯定是很浅显的,因为没有说出是否拦截、是否分发、是否消费的各种条件,没有涉及到各种action的分发情况,上面说的默认分发只是针对action_down的,因为view/viewgroup各种super调用都是不进行分发、拦截、消费的,所以在没找到处理touch事件的view时候,是一直往上层view传递的,一直传到activity里面,下面我们再来整理一下:
如果viewgroup不进行分发,那么
action_down、action_move和action_up只会执行到viewgroup的dispatchTouchEvent,不分发的条件是dispatchTouchEvent直接返回true或false,true和false的区别是true会执行action_down、action_move和action_up,而如果直接返回false只会执行到action_down。并且后续的viewgroup的onInterceptTouchEvent后续方法都不会被执行到。
关于为什么view/Viewgroup的dispatchTouchEvent返回true的时候三个action都能执行到,而返回false的话,只能执行到action_down,这个需要到view/Viewgroup的父类中dispatchTouchEvent找答案,该方法中会在action_down的时候调用dispatchTransformedTouchEvent方法,而该方法是通过子view的dispatchTouchEvent方法的返回值来决定父类的dispatchTransformedTouchEvent方法的返回值,而dispatchTransformedTouchEvent的返回值会决定mFirstTouchTarget是否为空,所以在action_down的过程中实际中通过子view的dispatchTouchEvent方法返回值来确定mFirstTouchTarget是否为空。这里贴出viewgroup中dispatchTransformedTouchEvent方法的删减代码:
private boolean dispatchTransformedTouchEvent(MotionEvent event, boolean cancel, View child, int desiredPointerIdBits) { ------------------ //省略了cancel部分的代码 ------------------------ //如果child为空,直接调用自己的dispatchTouchEvent方法,此时自己就相当于一个view,touch事件走自己的 if (child == null) { handled = super.dispatchTouchEvent(transformedEvent); } else { final float offsetX = mScrollX - child.mLeft; final float offsetY = mScrollY - child.mTop; transformedEvent.offsetLocation(offsetX, offsetY); if (! child.hasIdentityMatrix()) { transformedEvent.transform(child.getInverseMatrix()); } //返回值直接通过孩子来获取返回值 handled = child.dispatchTouchEvent(transformedEvent); } transformedEvent.recycle(); return handled;} 所以如果view/viewgroup的dispatchTouchEvent方法返回false,表示在action_down的时候,父类的dispatchTransformedTouchEvent方法返回false;如果返回true会调用addTouchTarget方法,给mFirstTouchTarget设置值:
private TouchTarget addTouchTarget(@NonNull View child, int pointerIdBits) { final TouchTarget target = TouchTarget.obtain(child, pointerIdBits); target.next = mFirstTouchTarget; mFirstTouchTarget = target; return target;} 紧接着在在后面又会调用了:

这句只有在view/viewgroup的dispatchTouchEvent返回false的时候,才会走这里,所以后面的action_move和action_up都会走这里,而此时传入的child=null,从上面代码可以看到,直接调用了父类的dispatchTouchEvent方法。所以从这里不难看出在view/viewgroup的dispatchTouchEvent返回false的时候直接调用了父类的dispatchTouchEvent方法,因此只有action_down事件。
面试官:如果我只想有view的拖拽事件,而不想要view的点击事件,让你重写这个view的拖拽怎么设计
其实这道题考察大家对view的dispatchTouchEvent和view的onTouchEvent事件的处理流程,上面已经分析了想要view能执行到view的touch事件,那么必须要求view的dispatchTouchEvent返回true,而dispatchTouchEvent返回true要么是dispatchTouchEvent直接返回true或者view的onTouchEvent返回true。如果从效率上看,直接将dispatchTouchEvent返回true就ok,而不需要再去关心onTouchEvent方法。
viewgroup拦截
关于拦截无非就是拦截或不拦截,而拦截的条件是返回true,不拦截是返回false或返回super.onInterceptTouchEvent,默认的super是返回false的,因此可以用super表示不拦截
viewgroup拦截实际是通过在dispatchTouchEvent方法中,设置intercepted变量,如果在拦截方法里面返回true,那么intercepted为true,如果为true则在action_down的时候mFirstTouchTarget=null,那么此时是直接调用dispatchTransformedTouchEvent传入的child=null,因此将事件交给了super.dispatchTouchEvent,此时把它当成一个view来处理了。
面试官:有个viewgroup,里面有个view,如果view在dispatchTouchView中不分发事件,并且只在action_move中拦截touch事件向下分发,说说viewgroup到view的各个action是如何分发的?
文末
初级工程师拿到需求会直接开始做,然后做着做着发现有问题了,要么技术实现不了,要么逻辑有问题。
而高级工程师拿到需求会考虑很多,技术的可行性?对现有业务有没有帮助?对现有技术架构的影响?扩展性如何?等等…之后才会再进行设计编码阶段。
而现在随着跨平台开发,混合式开发,前端开发之类的热门,Android开发者需要学习和掌握的技术也在不断的增加。
通过和一些行业里的朋友交流讨论,以及参考现在大厂面试的要求。我们花了差不多一个月时间整理出了这份Android高级工程师需要掌握的所有知识体系。你可以看下掌握了多少。
混合式开发,微信小程序。都是得学会并且熟练的
这些是Android相关技术的内核,还有Java进阶
高级进阶必备的一些技术。像移动开发架构项目实战等
Android前沿技术;包括了组件化,热升级和热修复,以及各种架构跟框架的详细技术体系

以上即是我们整理的Android高级工程师需要掌握的技术体系了。可能很多朋友觉得很多技术自己都会了,只是一些新的技术不清楚而已。应该没什么太大的问题。
而这恰恰是问题所在!为什么别人高级工程师能年限突破30万,而你只有十几万呢?
就因为你只需补充你自己认为需要的,但并不知道企业需要的。这个就特别容易造成差距。因为你的技术体系并不系统,是零碎的,散乱的。那么你凭什么突破30万年薪呢?
我这些话比较直接,可能会戳到一些人的玻璃心,但是我知道肯定会对一些人起到点醒的效果的。而但凡只要有人因为我的这份高级系统大纲以及这些话找到了方向,并且付出行动去提升自我,为了成功变得更加努力。那么我做的这些就都有了意义。
喜欢的话请帮忙转发点赞一下能让更多有需要的人看到吧。谢谢!
以上系统大纲里包含的所有技术资料,我这里都有的。可以免费分享给有需要的朋友!
,并且付出行动去提升自我,为了成功变得更加努力。那么我做的这些就都有了意义。
喜欢的话请帮忙转发点赞一下能让更多有需要的人看到吧。谢谢!
以上系统大纲里包含的所有技术资料,我这里都有的。可以免费分享给有需要的朋友!
转载地址:http://nfpoz.baihongyu.com/